Chapter 1 - Essence of linear algebra
transcribed by Martijn Benjamin (appeltje-c) from the "Essence of Algebra" Video Series
Working in 3D space involves understanding linear algebra:
"Linear algebra is the branch of mathematics concerning linear equations"
Vector
The fundamental root-of-it-all building block in linear algebra is the Vector.
What a Vector is
There are three distinct ideas about what a vector is:
Physics perspectiveVectors are arrows pointing in space. The vector is defined by its length and the direction it is pointing. As long as these two facts stay the same it is the same vector, wherever you move it around. Vectors in the flat plane a two-dimensional and those sitting in broader space are three-dimensional.
Computer science perspectiveVectors are ordered lists of numbers. In other words, in this context, a vector is simply the name for list and the length of the list gives it it's dimensions. A list of two numbers is a 2 dimensional vector.
Mathematical perspectiveGeneralizes both these physics and computer science views, basically saying that a vector can be anything where there's a sensible notion of adding two vectors and multiplying a vector by a number.
Coordinate System
In linear algebra with geometry in mind we can think of a vector as an arrow inside a coordinate system (an xy-plane) with the start of the vector sitting at the origin (0,0). In linear algebra it is almost always the case that the vector will be rooted at the origin. To translate these arrows in space to the list of numbers point of view we use the coordinates of the vector.
Axis & Grid
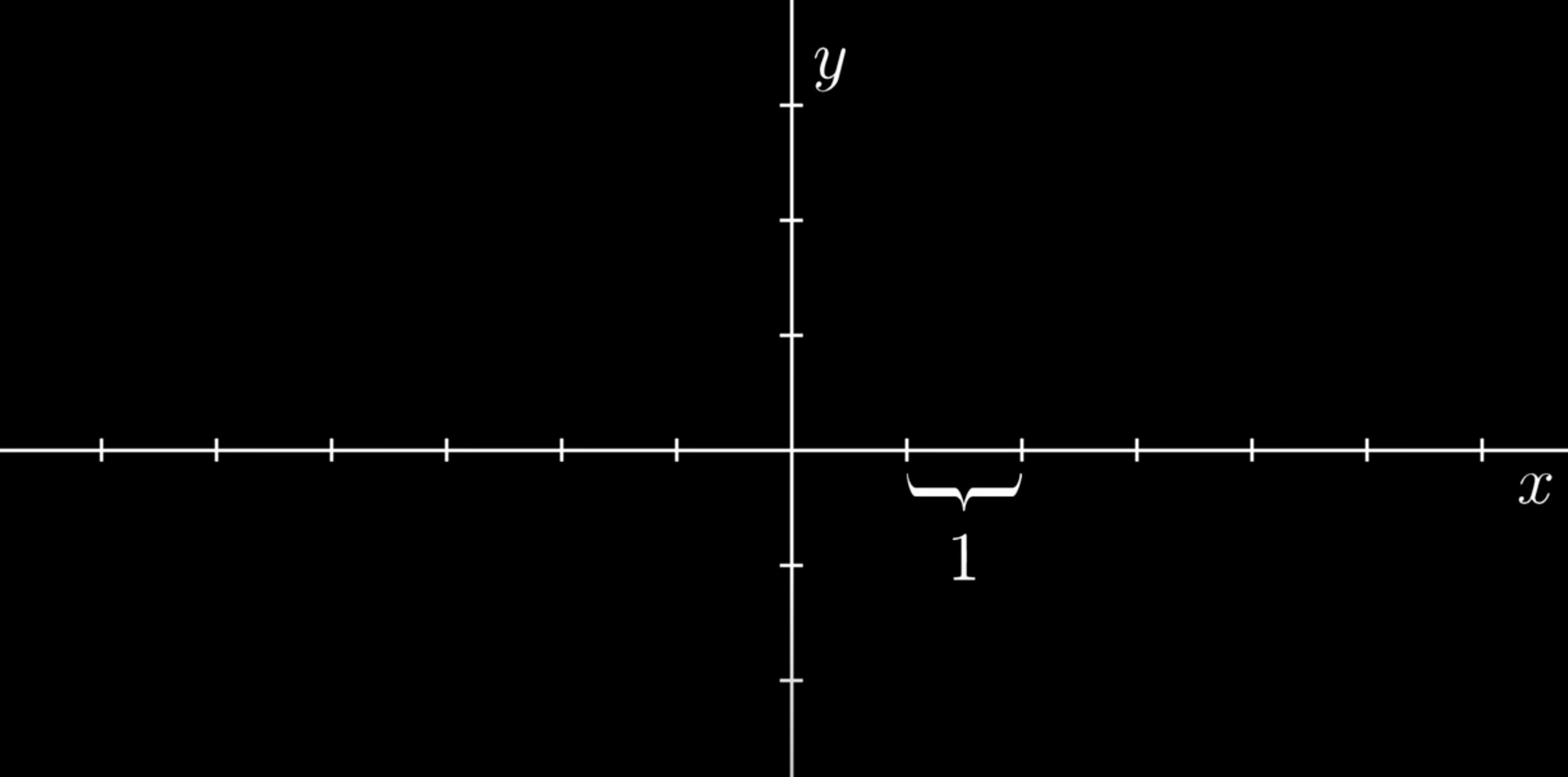
The coordinate system consists of a horizontal line called the x-axis and a vertical line called the y-axis. The place where they intersect is called the origin (the center of space, the root of all vectors. We add tick marks with the same distance (of choice) on each axis. You can draw lines from these tick marks to create a 2D grid.
Grid with tick marks of chosen distance
Extended with gridlines
Coordinate number pairs
The coordinates of a vector is a pair of numbers that tell you how to get from the origin to the tip. The first number tells you how far to move on the x-axis with positive moving to the right and negative numbers moving to the left. The second how far on the y-axis with positive numbers moving up and negative numbers moving down.
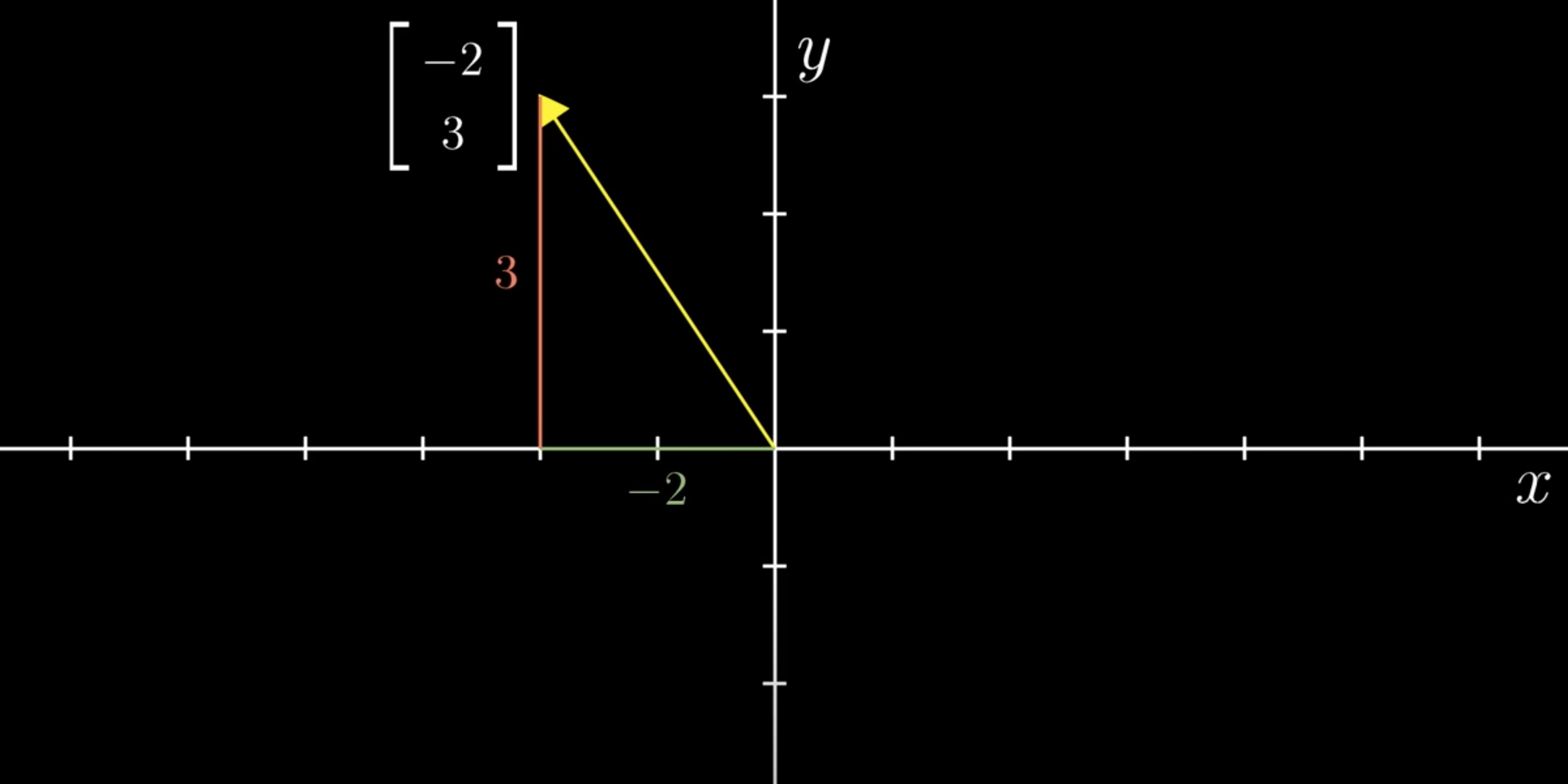
To distinguish vectors from points we write this pair of number vertically with square brackets around them. Every pair of numbers gives you one and only one vector and every vector is associated with one and only one pair of numbers.
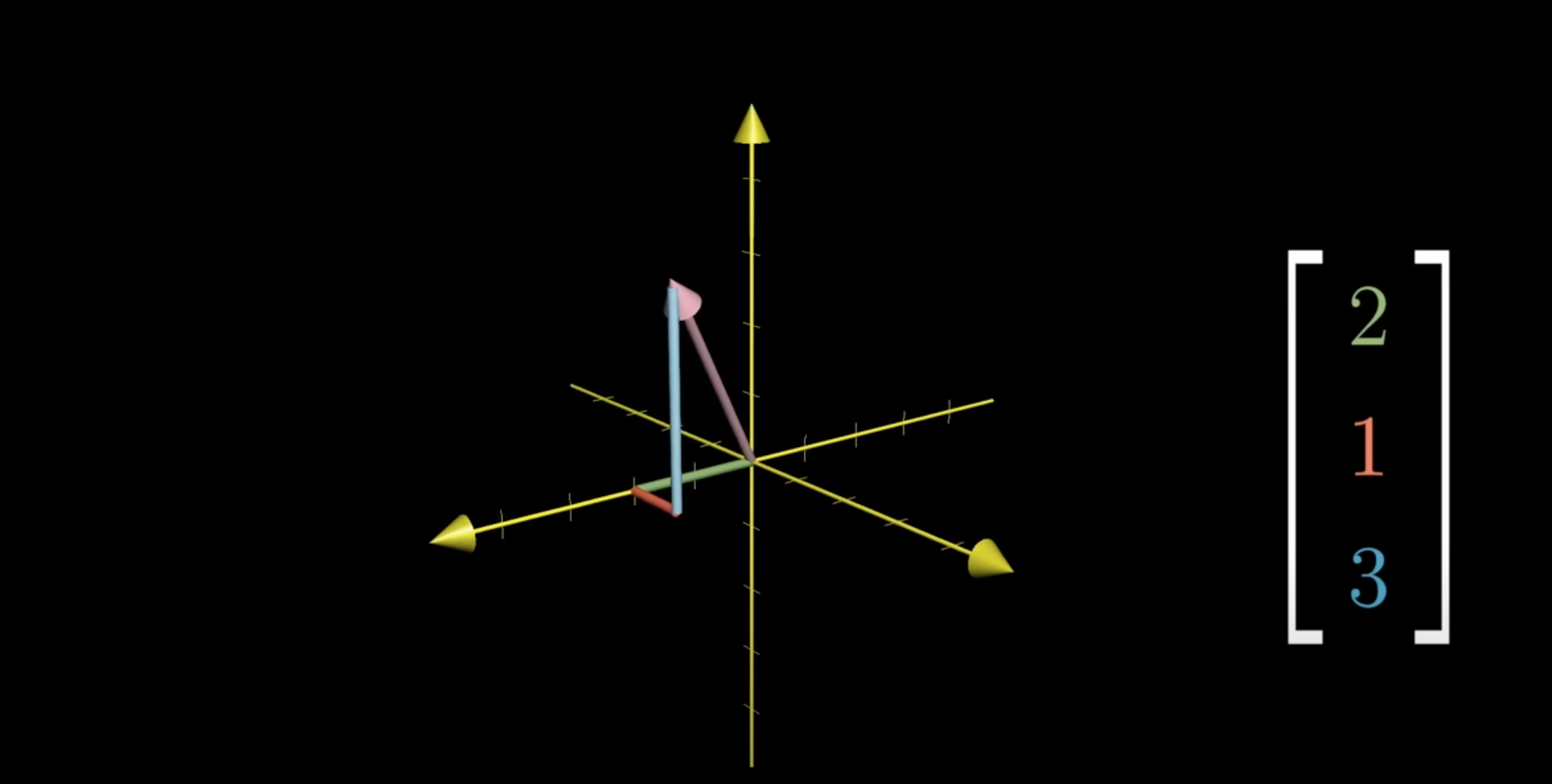
3 Dimensions
With three dimensions you add a third axis called the z-axis which is perpendicular to both the x and y axis for which we associate the vector with an ordered triplet of numbers. The first for the x-axis, the second the y-axis and the third the z-axis. Also here, every triplet of numbers gives you one unique vector in space and every vector in space gives you exactly one triplet of numbers.
Linear algebra operations
Every topic in linear algebra centers around vector addition and multiplication by numbers
Vector Addition
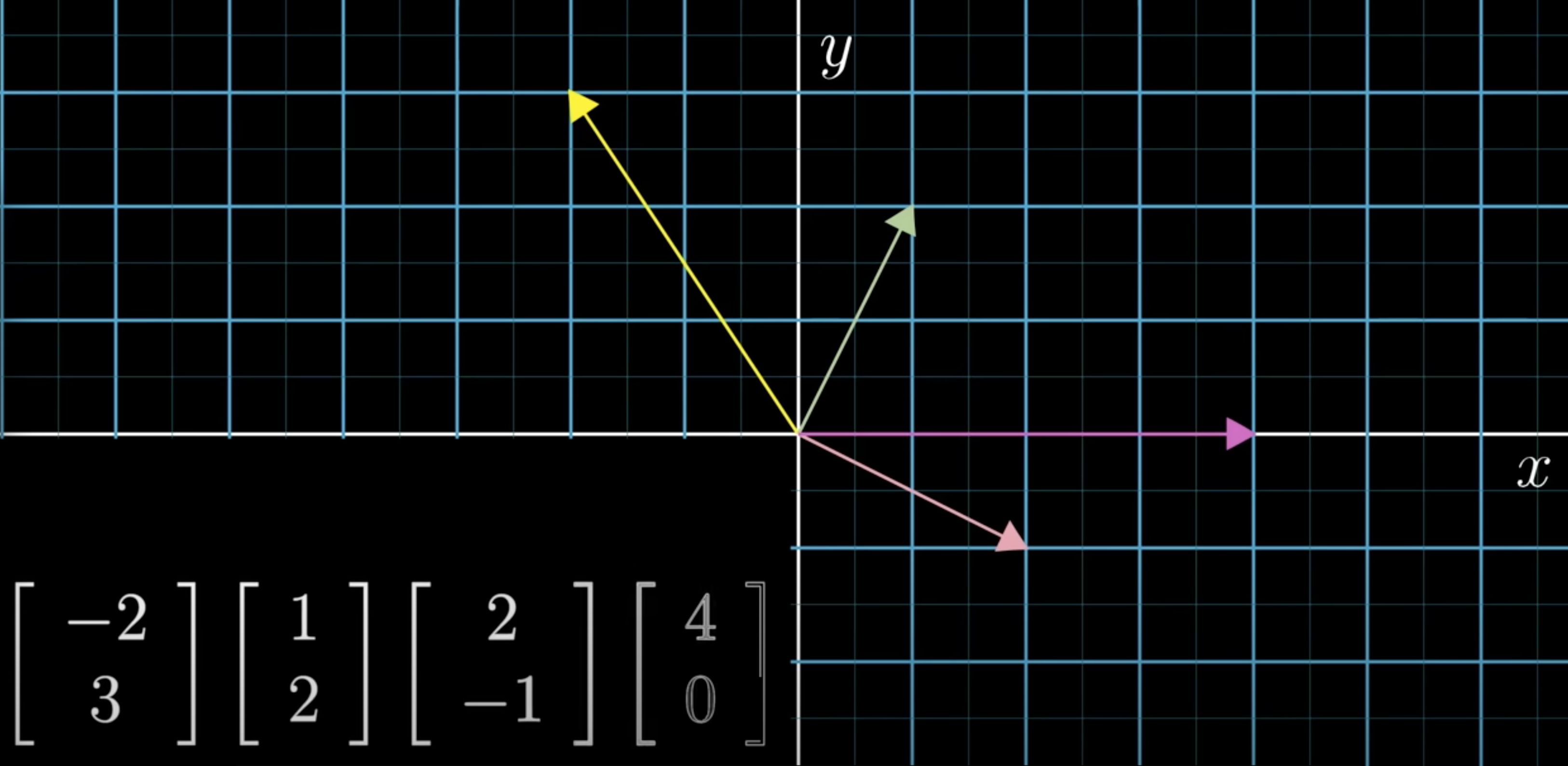
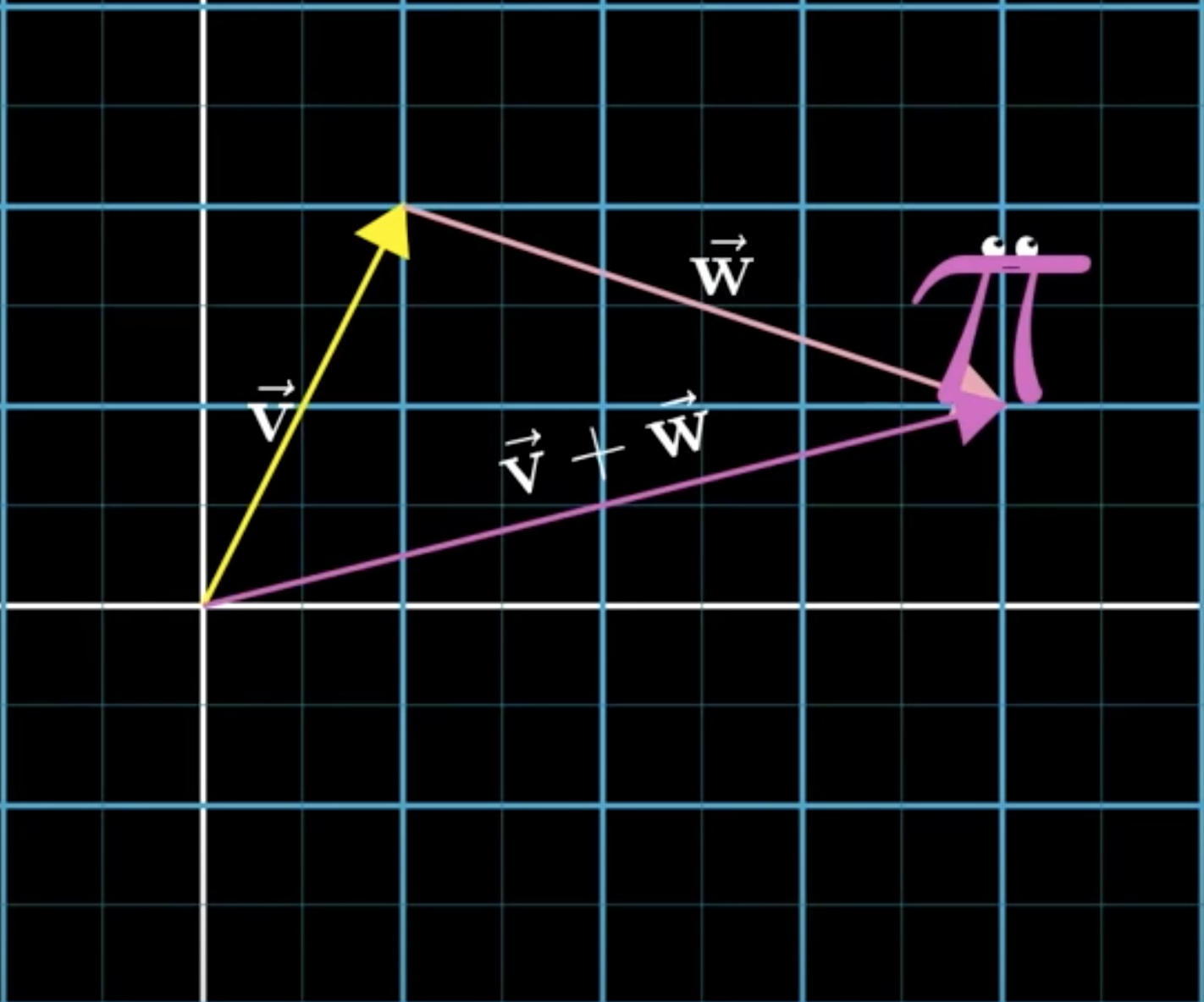
In the next image you see two vectors, one pointing up and a little to the right and the other one pointing right and down a bit.
To add these two vectors, move one vector so that it's origin moves on to the tip of the other. Drawing a line from the origin to the new tip location of the vector you moved is the sum of the two vectors.
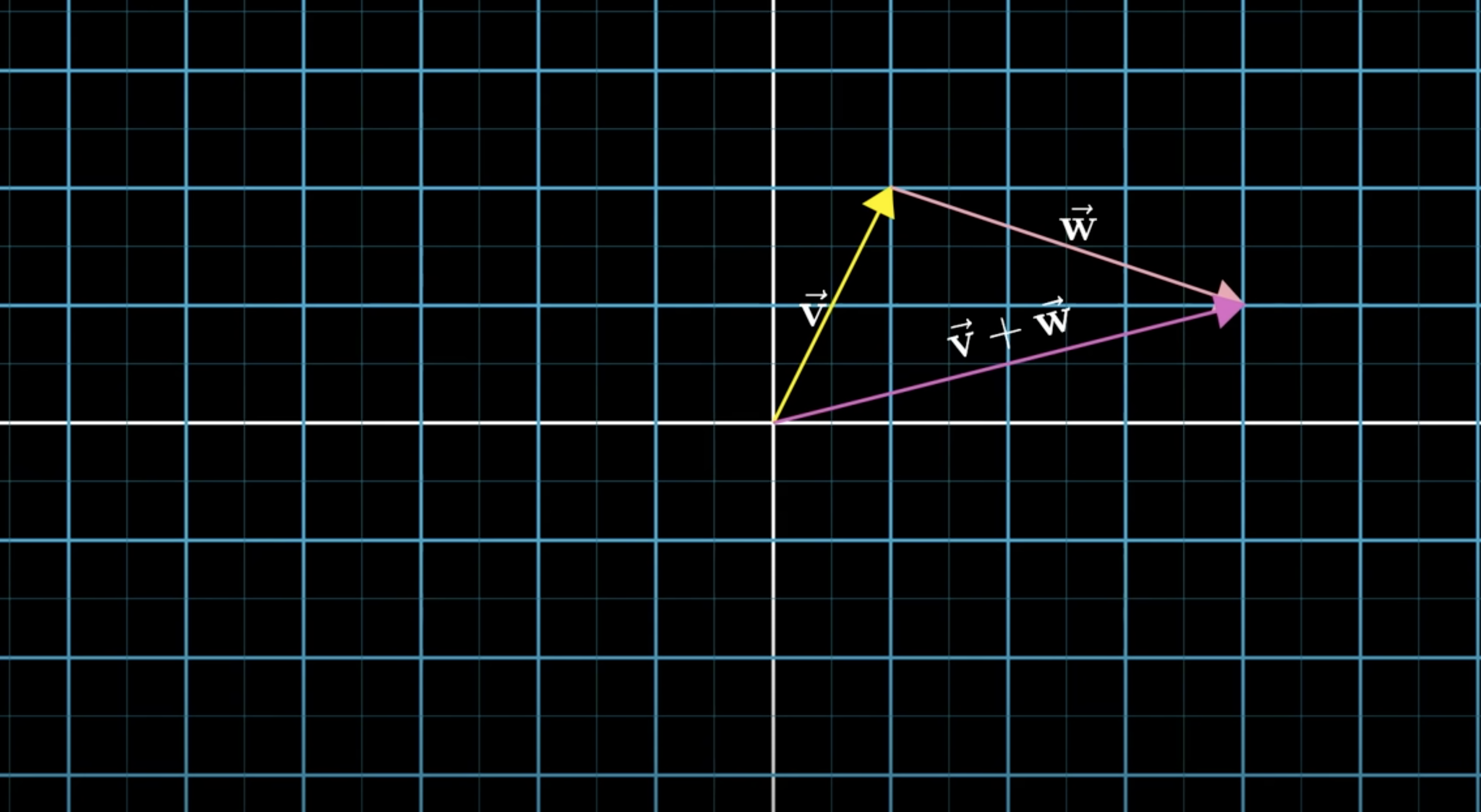
This definition of addition is to only time in linear algebra where we let vectors be moved away from their origin.
Why do we define addition of vectors this way? Why do we not for example add the two tips of the vectors without moving them?
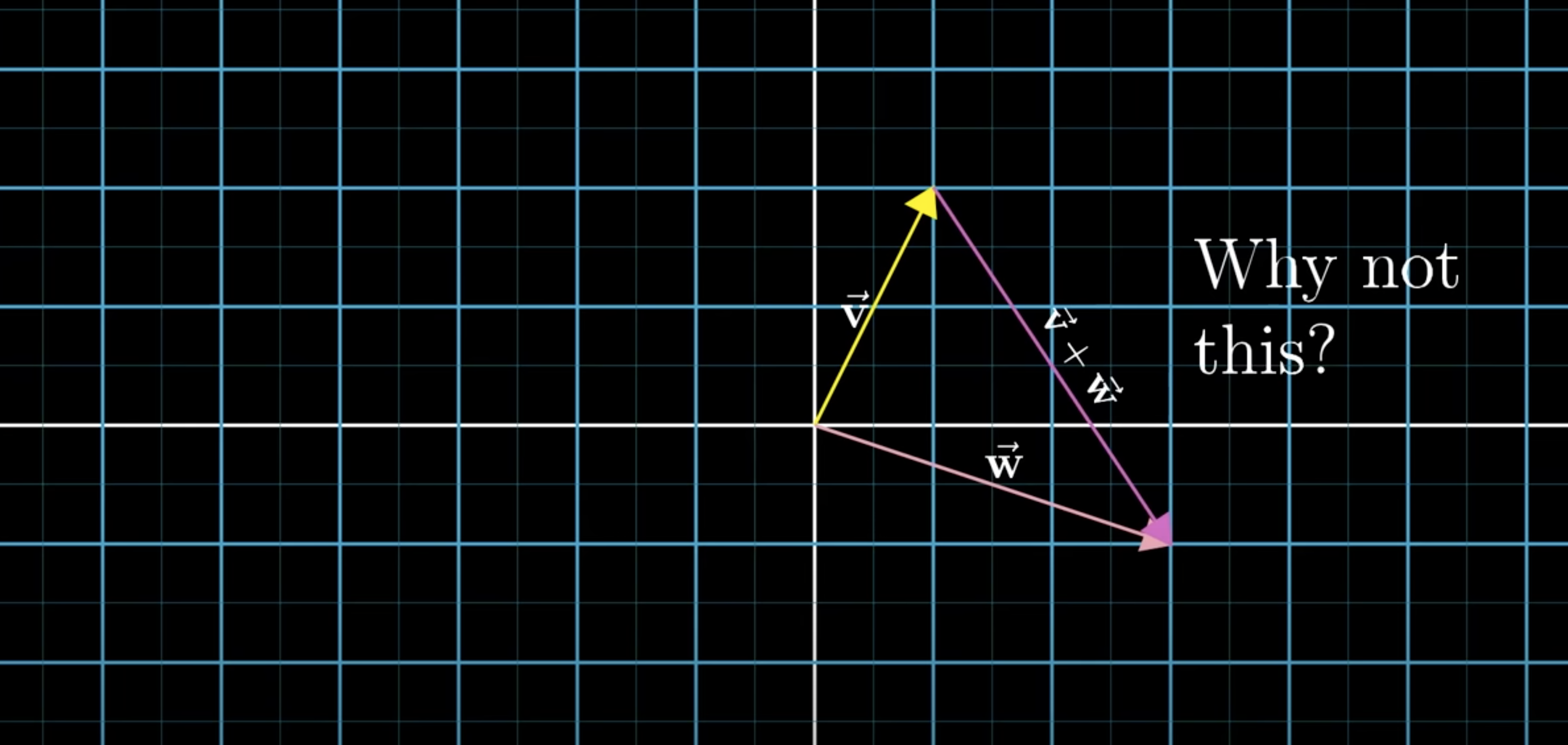
The way we can think about this is that each vector represents a certain movement in space, a step with a certain distance and direction in space.
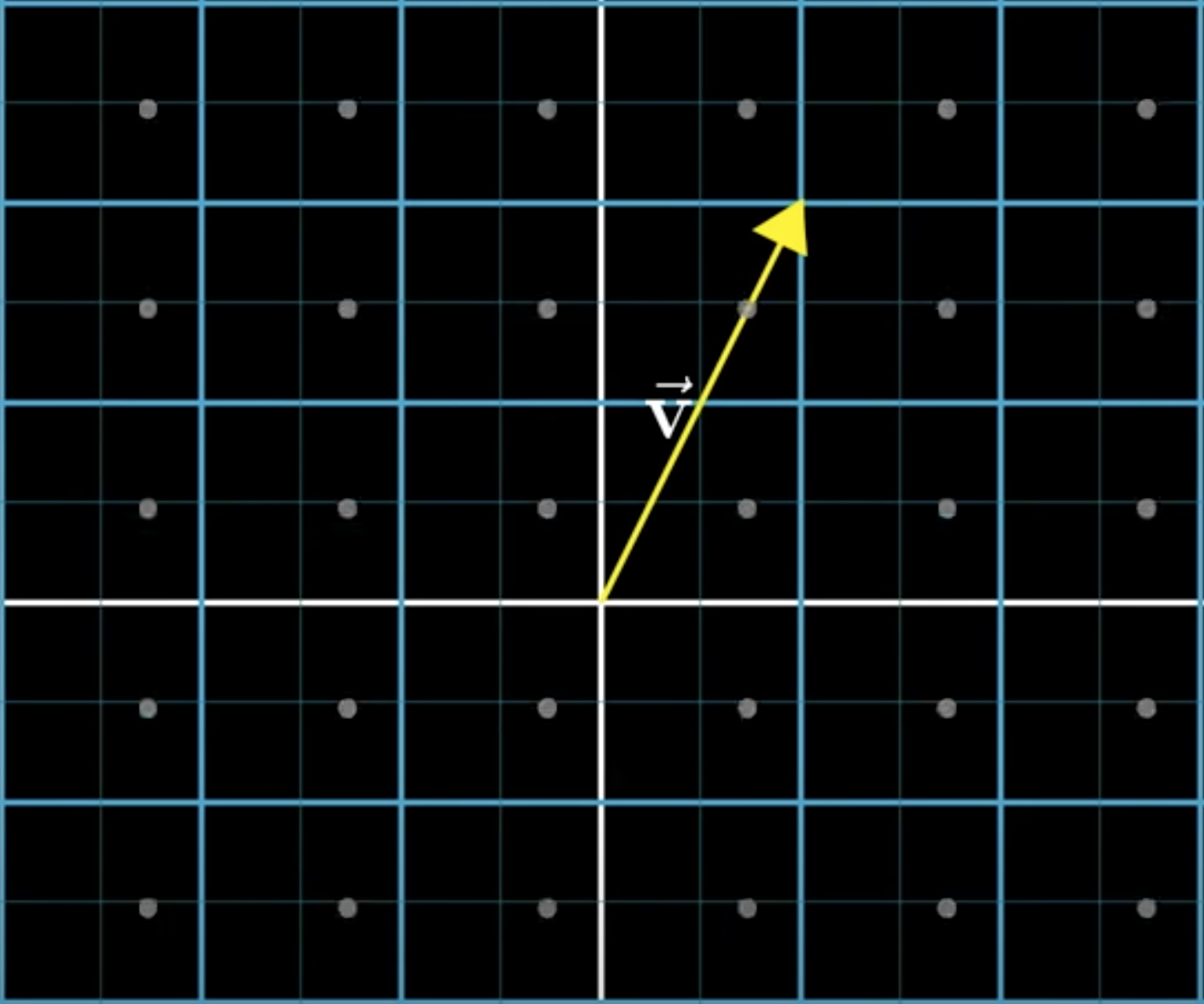
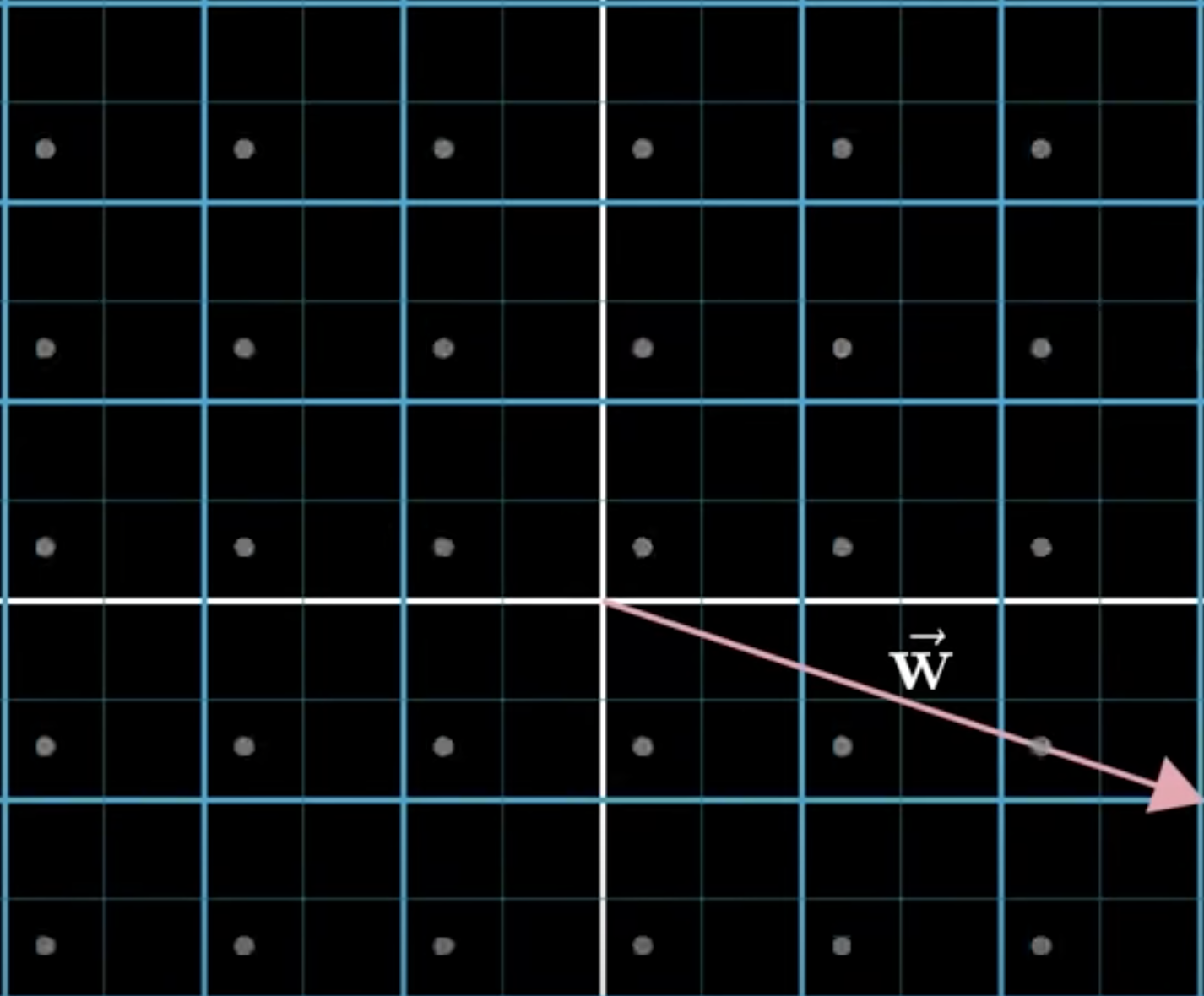
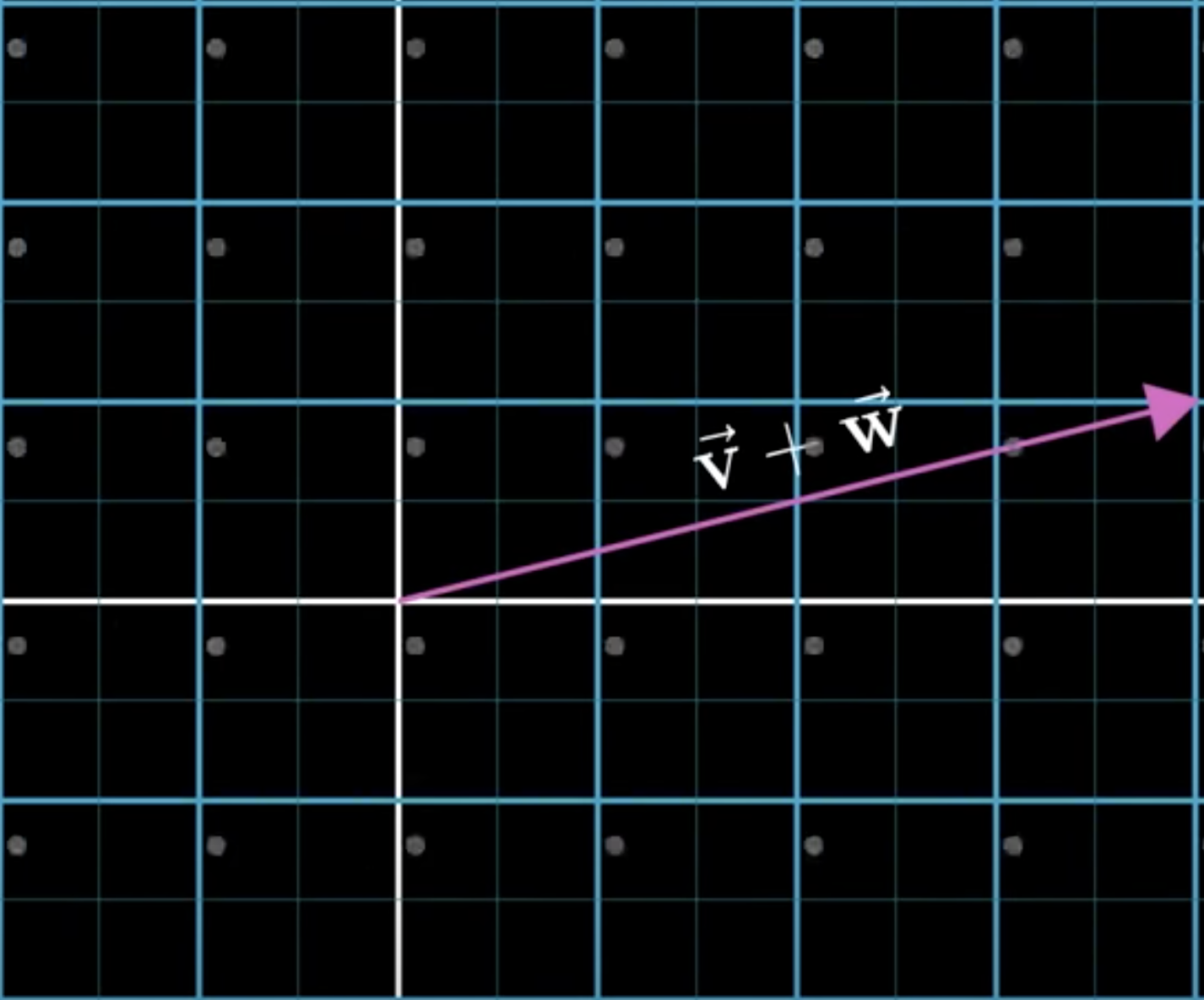
If you take a step along the first vector and then take a step in the direction and distance described by the second vector the overall effect is the same as if you moved along the sum of those two vectors.
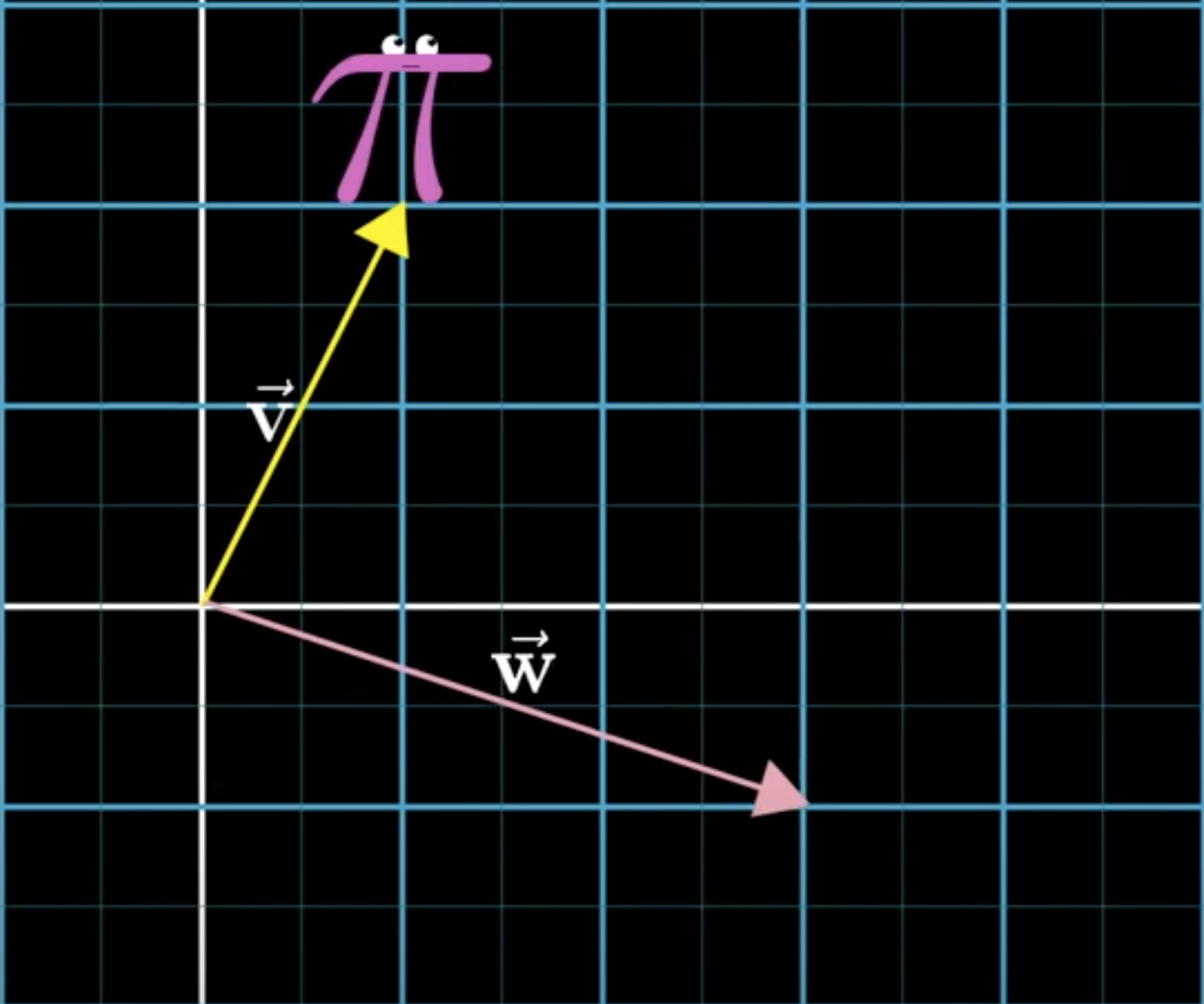
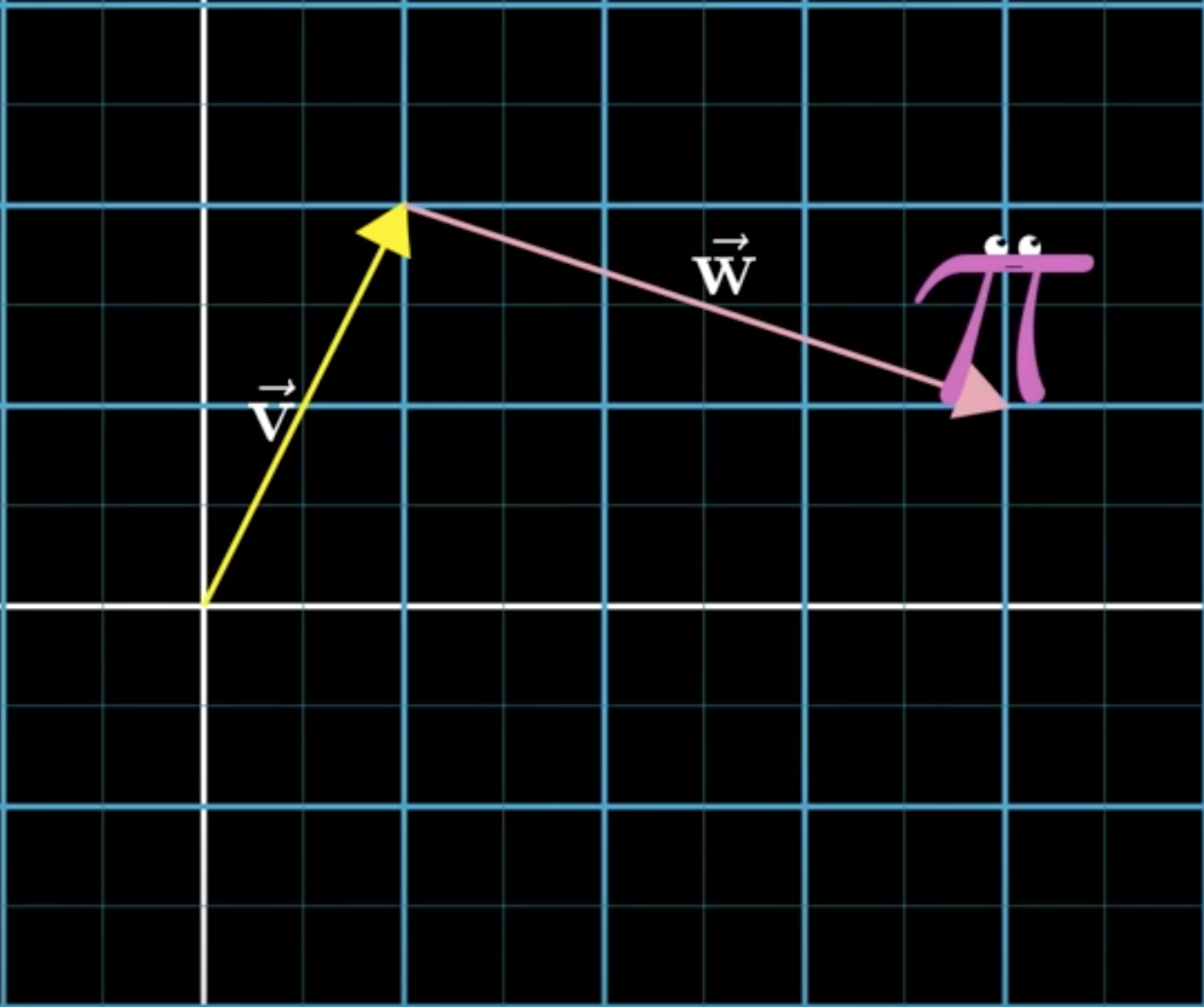
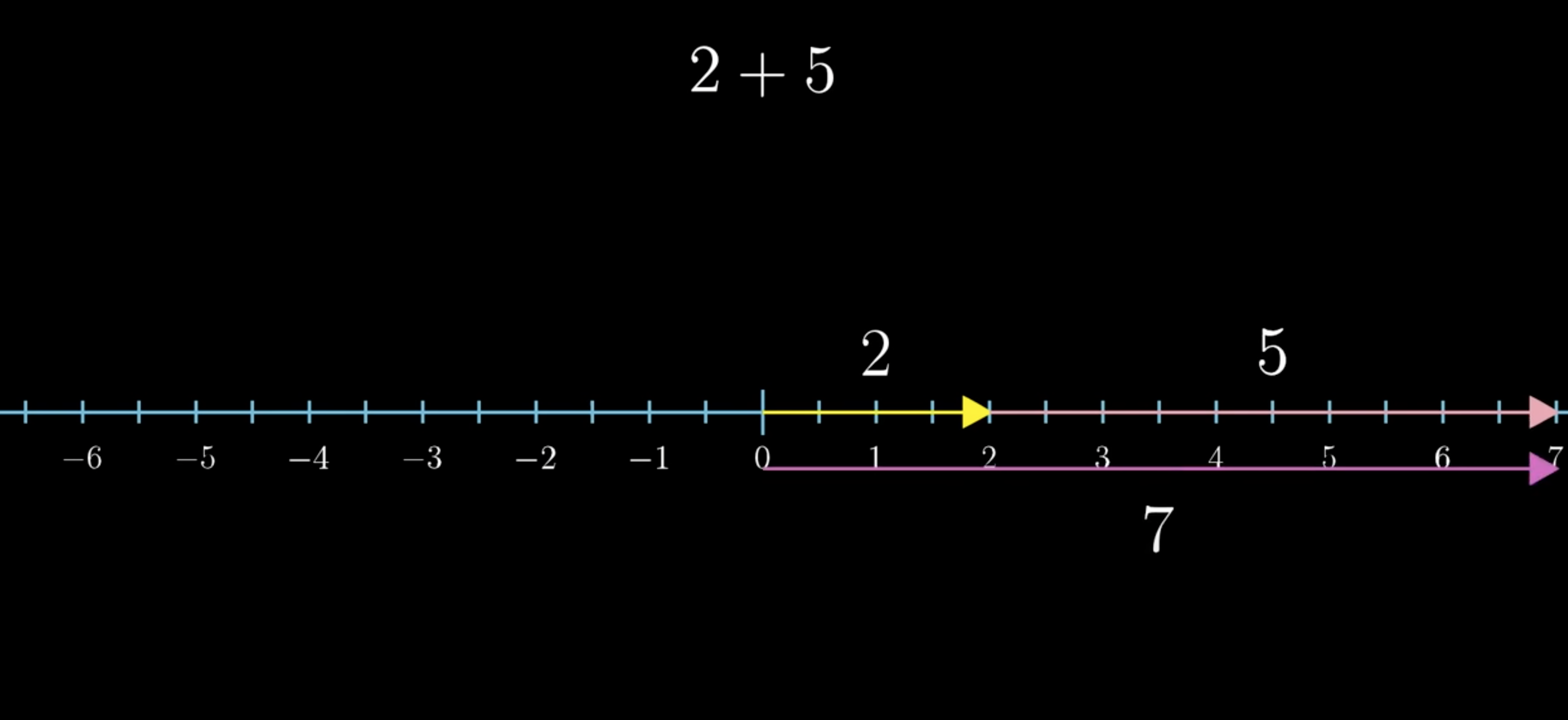
You can think of this as an extension of how we think about adding numbers on a number line.
One way we teach about this, say with 2 plus 5, is to think of moving two steps to the right followed by another five steps to the right. The overall effect is the same if you took seven steps to the right.
Let's look at how vector addition looks numerically.
The first vector has coordinates 1, 2 The second vector has coordinates 3, negative 1
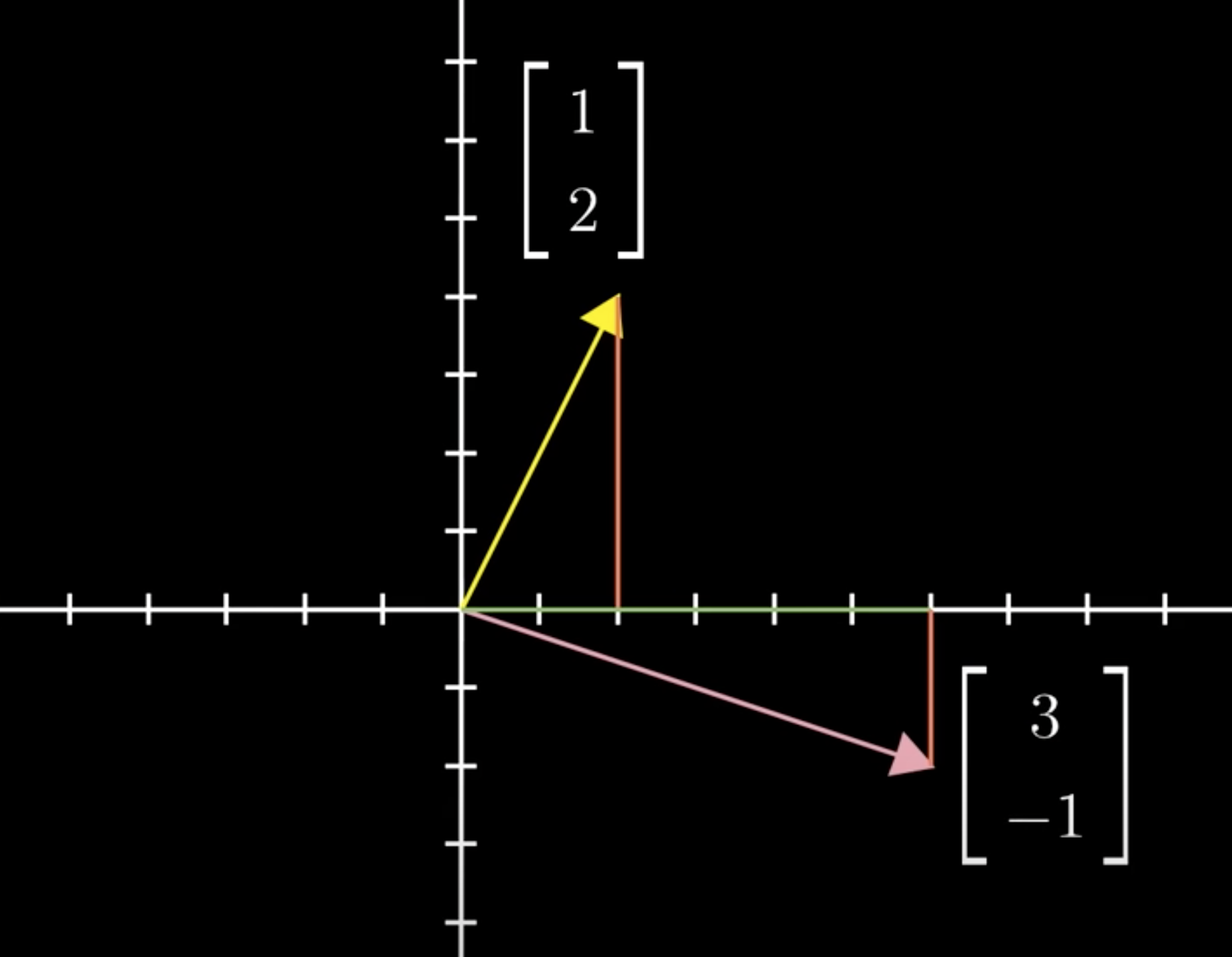
When you take the vector sum using the tip to tail method you can think of a four-step path from the origin to the tip of the second vector.